6. Labyrinter i chartres stil
Det mest iøjnefaldende ved Chartres Labyrinten i Chartres fra år 1200 er de smalle tunger på 90° og 180° længde som mødes symmetrisk ved kvadrantlinierne 90°, 180°, og 270°.
En labyrint i chartres stil bør opfylde følgende retningslinier:
- den består af smalle tunger 90° og 180° lange
- der er symmetri i kvadrantlinierne 90°, 180°, og 270°
- der er 2, 1, eller 0 radiærbaner i 0° og kun her
Kvadratisk og cirkulær
Labyrinten kan være cirkulær eller kvadratisk eller rektangulær eller andre former. Størrelsen på pladsen i midten er efter behov.
Vi vil her se på nogle eksempler på labyrinter i chartres stil. De er mindre end den store ægte Chartres Labyrint. Figurerne vender med 0° og 90° som i matematikken, og gangforløb til venstre (med uret) som i den ægte Chartres.
Symboler og mål
Se afsnittet om labyrinter i roma stil.
Indholdsfortegnelse for figurer
Fig.
ch2: ch3 system i Si8-2 og Si9-3
Fig.
ch3: ch5R1, ch5R2, og ch5Ø i bl.a. Si12-2 og Ci12-2
Fig.
ch4: ch6R og ch8C i bl.a. Si15-3, Ci14-2, Si18-2, Ci18-2
Fig.
ch5: ch10R og ch10Ø i Si24-4 og Si22-2
Fig.
ch6: ch8E og ch8F i Ci18-2, Ci18-2, og Si20-4
Fig.
ch7: ch5F som flervejs-labyrint i Si12-2 og Ci12-2
Fig.
ch8: Sammenligning mellem chartres ch5R1 og roma S13-3
Fig. ch1: Chartres
systemer
Der er her vist nogle eksempler over forslag til labyrinter efter chartres princippet. Disse labyrinter er alle mindre end den originale labyrint i Chartres (som er ch11). For overskuelighedens skyld er labyrinterne her vist i rektangulær symbolform. Labyrinter større end den ægte i Chartres fås som vist ved kombination og udbygning. Se også den udvidede Chartres labyrint i fig. C4.
ch3R er den mindste labyrint. Den er 3 baner bred, og har 1 radiær-bane fra yderkant mod inderkant.
ch5R er en udvidelse af ch3R. Med en 90° tunge i hver kvadrant som vist fås ch5R1, eller med 2 stk. 180° tunger fås ch5R2. Med yderligere udvidelse med 90° tunger og 180° tunger kan man få ch7R systemer og ch9R systemer osv. som ikke er vist her.
ch6R er dannet ved at kombinere ch3R og spejlvendt ch3R.
ch8R er dannet ved at kombinere ch3R og spejlvendt ch5R2.
ch9R er dannet ved at kombinere ch6R og spejlvendt ch3R.
ch10R er dannet ved at kombinere ch5R2 og spejlvendt ch5R2.
ch8C er dannet ved at kombinere spejlvendt ch3R og ch5R2. Radiær-bane kan have skarpe knæk.
ch10C er dannet ved at kombinere spejlvendt ch5R2 og ch5R2.
ch8E er dannet ved at kombinere ch3R og ch5R2.
ch10E er dannet ved at kombinere ch5R2 og ch5R2.
ch5Ø er dannet af ch5R2 ved at spejle den nederste 180° del og slette radiær-banen.
ch10Ø er dannet ved at kombinere ch5Ø og spejlvendt ch5Ø.
De viste ch-systemer kan bøjes eller knækkes til at danne cirkulære labyrinter eller labyrinter i kvadrater eller labyrinter i andre figurer.
ch8E og ch10E kan benyttes cirkulært men kan ikke benyttes til kvadrat på grund af en fællestern i radiærbanekrydset.
De 360° rundt er her 4-delt til 90°, 180°, 270°. Der kunne også laves systemer med fx 3-deling til 120° og 240° og andre inddelinger.
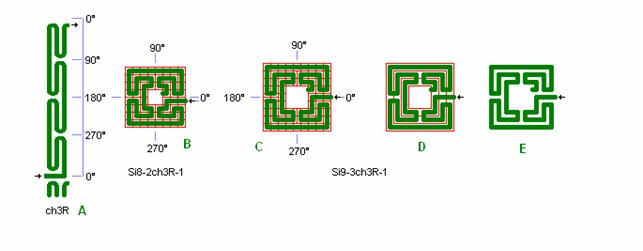
Fig. ch2: ch3 system i
Si8-2 og Si9-3
ch3 vist som kvadrat-labyrint, den mindste chartres labyrint.
I detail B er mindste størrelse en tern på 1. Det giver ikke fuldkommen tunge-symmetri i 0° kvadrantlinien. I C, D, og E er der fuldkommen tunge-symmetri ved at midterpladsen er udvidet fra 2 x 2 til 3 x 3 og ved at der er benyttet ½ tern ved tunger i 90°, 180° og 270° kvadrantlinier.
Med en tern = 1 x 1 m er banebredden = 1 m brutto og Si8-2 labyrinten et 8 x 8 m kvadrat med 2 x 2 m midterplads hvor banen ender indvendigt.
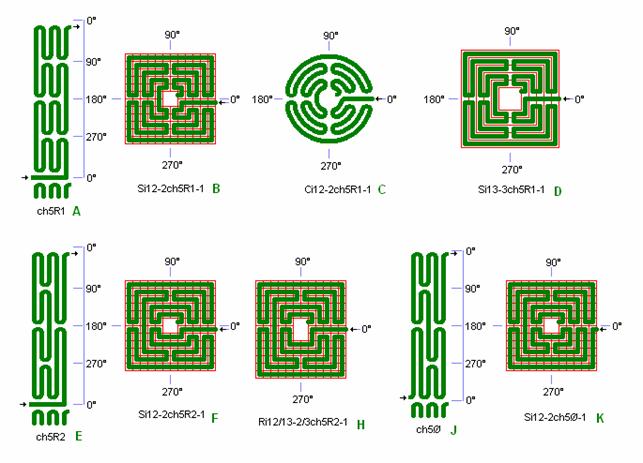
Fig. ch3: ch5R1,
ch5R2, og ch5Ø i bl.a. Si12-2 og Ci12-2
For ch5R1 er der i detail D skaffet fuldkommen tunge-symmetri ved at benytte ½ tern på samme måde som beskrevet for ch3R.
I detail H er ch5R2 vist i rektangulær form, så radiærbanen ligger midt i indgangssiden. Alle chartres labyrinter kan på denne måde uden videre strækkes til vilkårlig rektangulær form. (Dette kan være vanskeligt for roma labyrinter).
ch5R1 i detail A, B, C, og D gennemfører efter tur de 4 kvadranter, på delvis samme måde som var det en roma labyrint, blot bør en god roma labyrint have 4 radiær-baner. Se sammenligning med roma nedenfor i fig. ch8.
ch5R2 er måske mere i chartres stil ved at bevæge sig mere
over 180° med skiftevis tunger og linier
i kvadrantlinierne. Den har symmetri i tunger ved alle 4 kvadrant linier og
symmetri mellem 90° og 270°.
Ch5Ø i detail K er
uden radiær-bane i 0°. Herved går noget af symmetrien fra ch5R2 tabt.
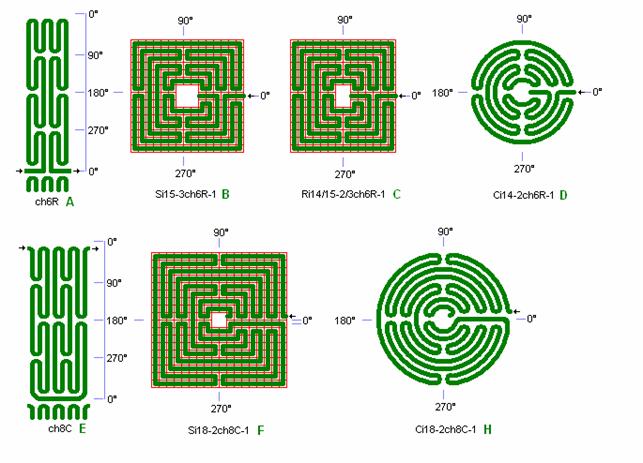
Fig. ch4: ch6R og ch8C
i bl.a. Si15-3, Ci14-2, Si18-2, Ci18-2
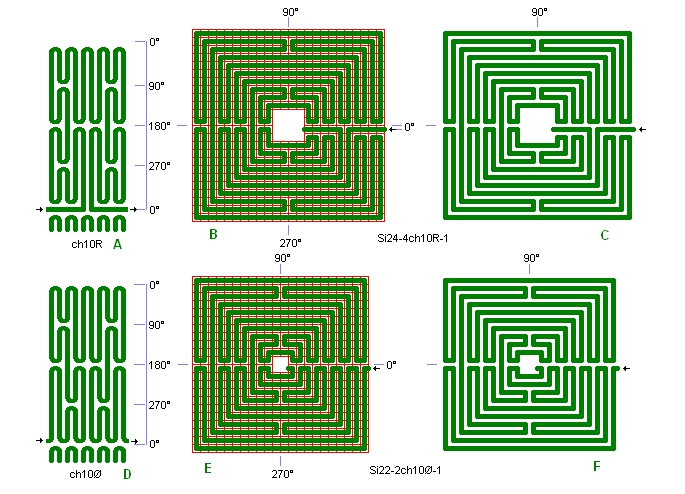
Fig. ch5: ch10R og
ch10Ø i Si24-4 og Si22-2
I 90° og 270° er der kun to tunger og mange linier. ch10Ø er uden radiær-bane i 0° og her mødes de mange tunger uden symmetri.
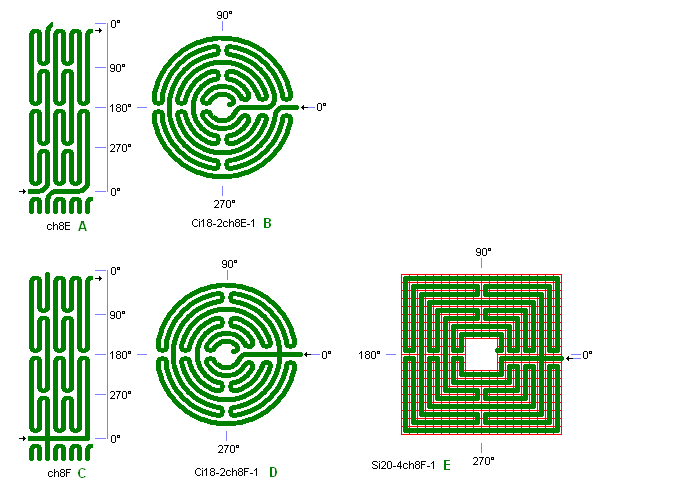
Fig. ch6: ch8E og ch8F
i Ci18-2, Ci18-2, og Si20-4
ch8E kan ikke uden videre benyttes som kvadrat-labyrint på grund af et sammenfaldende krydsningspunkt i radiær-banen i 0°. Hvis dette punkt ændres til en flervejs-labyrint som vist i ch8F, hvorved der opnås fuld symmetri i 0° kvadrant linien, kan ch8 også benyttes som kvadrat som vist i detail E.
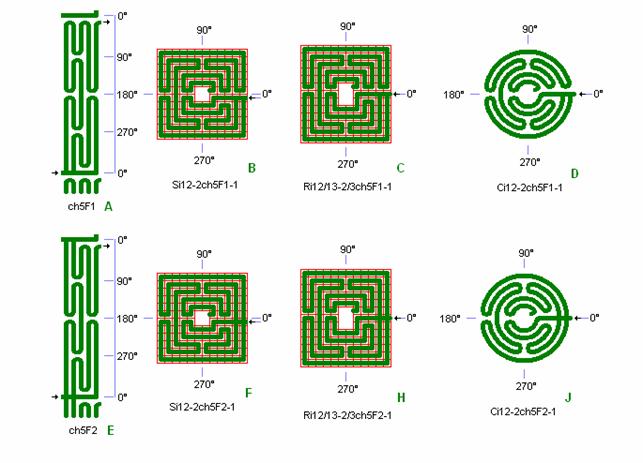
Fig. ch7: ch5F som
flervejs-labyrint i Si12-2 og Ci12-2
Vælger man i radiærbanen i ch5F1 at gå til venstre i bane nr. 2 eller i inderbanen kommer man blot tilbage ud igen. Yderbanen længst fra midten er den rigtige vej til midten.
ch5F2 er pænere symmetrisk om radiærbanen end chF1 og den er som flervejs-labyrint interessant til en speciel barneleg (eller kærestefolk leg): ”Du kan ikke fange mig”. I ch5F2 er der lige efter start 5 valgmuligheder. 2’ bane til højre fører til centrum, og man er fanget hvis man har en efter sig. Prøv den leg med dit 3-årige barnebarn.
Denne labyrint i detail F er benyttet som den ydre
flervejslabyrint-del i de store sammensatte Ariadne labyrinter i fig. ph1, fig. ph2,
fig. ph4, og benyttet i fig. ph5. Se også det skrevne om u-penetrable labyrinter.
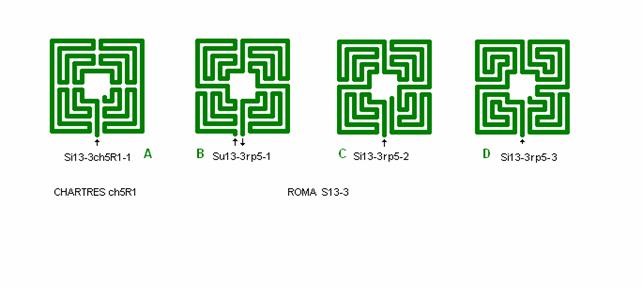
Fig. ch8:
Sammenligning mellem chartres ch5R1 og roma S13-3.
Roma gennemløber hver kvadrant for sig. Det gør denne Chartres ch5R1 også, dog ud ind ud ind. Chartres har kun 1 radiærbane, mens roma har 4 radiærbaner, en i hver kvadrantlinie.
Roma i B har både indgang og udgang i yderside. I C er dette ændret til slutmål i midten ved blot at føre ydersidens udgang ind til midten med yderligere en radiærbane, således at der er to radiærbaner ved indgangskvadranten. Dette princip ses også anvendt i nogle klassiske romerske labyrinter. Så er labyrint i D mere efter Roma-Piadena princip, se detail A med roma basics i fig. r2.
Indhold af øvrige afsnit:
5 Chartres Labyrinten i Chartres
7 Sammenlignende labyrint-eksempler