4. Labyrinter i roma stil
Roma labyrinten er enkel og interessant og samtidig smuk og anvendelig i mange sammenhænge til fx flisebelægning og gulvmosaik. Navnet roma (internationalt for Romerriget) er her brugt for labyrinter i romersk stil som følger de nedenfor angivne principper. Roma-Piadena Labyrintens princip kan benyttes til en hel serie af labyrinter.
Hovedprincip for kvadratiske og cirkulære roma labyrinter:
- labyrinten er delt tydeligt op i 4 kvadranter med 4 radiærbaner i de 4 kvadrantlinier
- kvadrant 2 og 3 er en præcis gentagelse af kvadrant 1
- kvadrant 4 er enten = kvadrant 1 eller en variant der tilsyneladende ligner
Fire ens kvadranter giver indgang såvel som udgang i yderkant af labyrinten.
Når labyrinten har slutmål i midten skal kvadrant 4 være anderledes og ”vende” den udadgående gangretning til ind mod midten.
- Vi så ved analysen af den ægte Roma-Piadena Labyrint at gangforløbet i hver kvadrant fulgte et bølgemønster og at kvadrantens yderkant som en ”bølgeryg” var en ubrudt bane, se fig. r2 detail A.
Disse principper er benyttet til at konstruere et system af roma kvadranter til kvadrant 1 i fig. r2 og kvadrant 4 i fig. r3 og fig. r4 efter bølgeformer vist i fig. r1.
Indgang for oven
Labyrinterne her vender på samme måde som den ægte Roma-Piadena Labyrint er afbildet, dvs. indgang er foroven på tegningen, og når man går ind har man 1. kvadrant på højre hånd og 4. kvadrant på venstre hånd (dvs. omløbsretning modsat uret). (Afsnit 3A viser også lidt anderledes typer romer labyrinter).
Både indgang og udgang i yderkant
Som vist blandt de følgende eksempler kan roma labyrinten foruden at have slutmål i midten ligesom troja og chartres også have både indgang og udgang i ydersiden, se fx fig. r16. Gangforløbet er da at man i hver kvadrant gennem de bølgende gange med frygt bevæger sig ind mod midten hvor uhyret lurer, for lige før man bliver grebet af dens kløer at haste ud af den næste radiærbane i kvadrantlinien for så at begynde på den næste kvadrant. Man viser sit mod ved at trodse disse farer og løbe gennem hele labyrinten. Disse labyrinter har 4 ens kvadranter og er således meget nemmere at konstruere og tilpasse end labyrinter med slutmål i midten.
Længde- og areal-enheden er en tern, fx 1 x 1 meter, 1 = brutto banebredde, eller 1 = afstand fra banemidte til banemidte.
Labyrint-betegnelse i dette skrift, symboler
Su11-1rp5-1 betyder: S = kvadrat (Square), u = udvendig udgang, 11 = 11 stor ydre mål, 1 = 1 stor midterplads, rp = roma(-piadena) model, 5 = 5 sving i bølge, 1 = løbenr.
Ci18-2ch: C = Cirkel, i = indvendig slutmål (hvor banen ender), ch = chartres model.
Ri14/15-1tr: R14/15 = Rektangel 14 x 15, tr = troja.
Indholdsfortegnelse for figurer
Fig.
r3: 4. kvadrant efter bølge H
Fig. r4:
4. kvadrant efter bølge K
Fig.
r15:Form AABA Si9-1, Si17-1
Fig. r16: Diverse roma
labyrinter
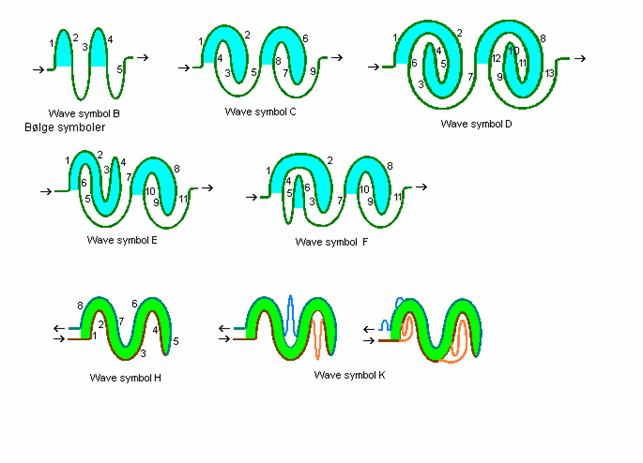
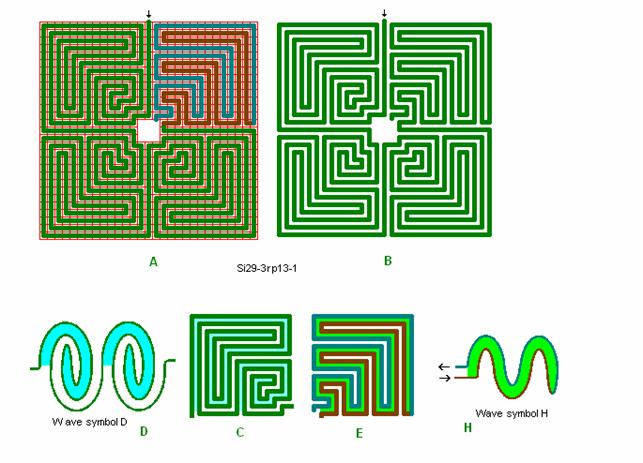
Fig. r1: Bølgefigurer
Labyrint bølge-grundfigurer.
I Roma-Piadena Labyrinten består hver kvadrants gennemløb af en bølgefigur. I troja labyrinterne består hele labyrintens gennemløb af en bølgefigur. Der vil her blive benyttet de viste bølgefigurer.
Symbol B: ”den almindelige bølge”.
Forekommer i troja 1 med bølgedel 1 – 3.
Symbol C: ”styrtbrydning fra top (crest)”.
Forekommer i troja 2 med bølgedel 2 – 8. Forekommer i Roma-Piadena 1 – 3 kvadrant hvor man går fra 9 mod 1.
Symbol D: ”rullebrydning”.
Forekommer i troja 3 med bølgedel 2 – 12.
Symbol E: ”reflekteret styrtbrydning”.
Symbol F: ”overbrydning”.
Symbol H: ”slange-bølge”.
Forekommer i Roma-Piadena kvadrant 4.
Symbol K: ”slange-bølge med løs ham”.
De viste folder på ”bølge-hammen” på banen ind og på banen ud forekommer i varieret omfang i de roma labyrinter der er medtaget i det følgende.
I det følgende er der labyrint-eksempler på alle slags bølgeformer.
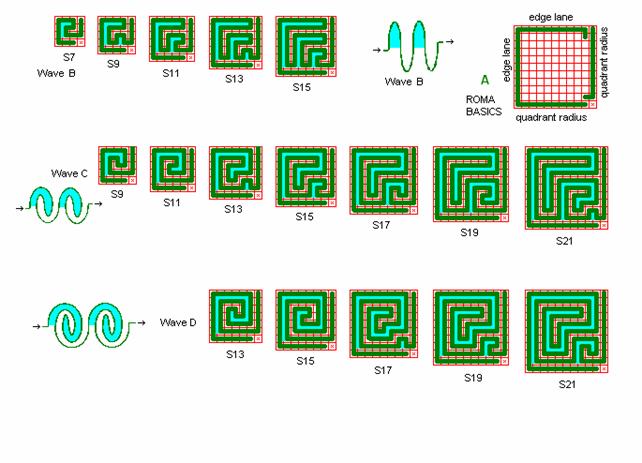
Fig. r2: 1. kvadrant
Roma kvadranter til 1. – 3. kvadrant i roma labyrinter.
Der er her tegnet 1. kvadrant med labyrintens midte nederst til højre.
Til en labyrint kan benyttes 4 ens kvadranter fx S11 drejet 0°, 90°, 180°, 270°, samlet om det fælles midtpunkt. Labyrinten bliver dermed 11 x 11 kvadrat stor og har både indgang og udgang i yderside, Su11, se Su11-1rp5-1 i fig. r16 i dette roma afsnit. Benyttes en speciel 4. kvadrant har banen slutpunkt i midten, Si11.
Kvadranterne er konstrueret ud fra de 3 grundlæggende bølgeformer B, C, og D, og ud fra et grundlæggende roma-piadena princip vist i detail A. Den mindste tegnede kvadrant er S7 med 1 bølge B. S15 har 3 bølger B, eller 1½ bølge C, eller 1 bølge D. Større kvadranter konstrueres på samme måde.
Den ægte Roma-Piadena Labyrint benytter S21 bølge C med 4 tern fra kvadranten taget til midterfeltet (som i alt er 3 x 3 tern).
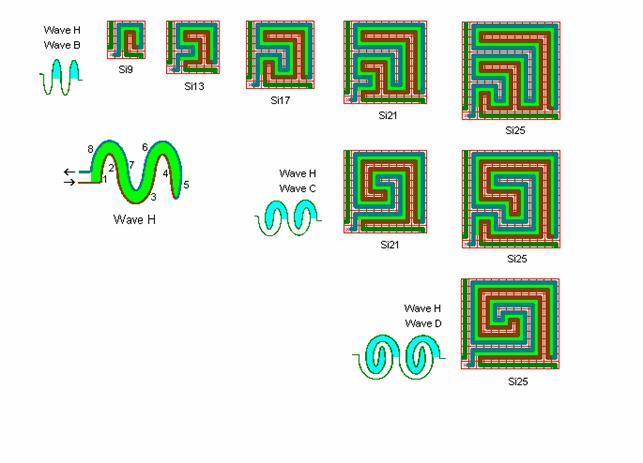
Fig. r3: 4. kvadrant efter bølge H
Roma kvadranter til 4. kvadrant i roma labyrinter med slutmål i midten.
Der benyttes bølgeform H, ”slange-bølgen”, dvs. ud og ind af samme vej, hvor slangen bølger efter henholdsvis bølgeform B, C, og D.
Da der skal benyttes en dobbeltlinie (både ud og ind) er der behov for en del areal-plads, så der fås ikke så mange forslag. Det kan således blive aktuelt at fravige dobbeltlinien og skifte til bølgeform K, som vist i eksempler, også for at få smukkere helhedsløsninger i roma labyrinten.
Sammenlign Si21 wave B med Roma-Piadena detail F i fig. Rp2 spejlvendt diagonalt.
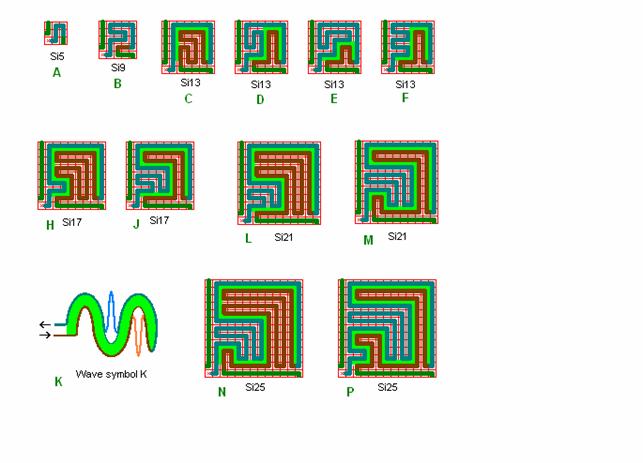
Fig. r4: 4. kvadrant
efter bølge K
Roma kvadranter til 4. kvadrant i roma labyrinter med slutmål i midten.
Der benyttes bølgeform K, dvs. der er afvigelser fra dobbeltlinien i slangebølgen H.
Bølge K vist i detail K med viste 2 småbølger er begge benyttet i L og N og med én småbølge i C, D, H, J, M, og P. Der er flere varianter som vist for Si13 i E og F.
Flere tilpasnings-varianter er vist i andre figurer med labyrinter.
Der er her tegnet 4 stk. Si13, men blot ved at lave små ændringer i fx detail C kan man få mange flere forslag, som så måske ligesom i detail F begynder at afvige lidt fra den regulære bølgeform.
Den lille Si5 i detail A er uden radiær-bane i 4. kvadrantlinie.
Si9 er desuden en normal dobbelt linie slange-bølge i en spejlvendt udgave i sammenligning med Si9 i fig. r3.
3+1 kvadranter =
labyrint
Kvadranter fra de 3 figurer med kvadranter (fig. r2 + r3, eller r2 + r4) kan så sammensættes til hele labyrinter. For at få et pænt udseende mellem 4. kvadrant og de øvrige kvadranter vil man dels vælge med omhu og dels ofte pusle med små ændringer i gangforløbet, som det fremgår af de viste eksempler i de næste figurer. (se fx fig. r9 sammenholdt med r10 og r11).
Også 4 helt forskellige kvadranter kan sammensættes til en labyrint, en mere varieret labyrint, men så er det ikke mere en roma labyrint efter principperne i dette afsnit. (En måske fejlagtig undtagelse er Wales roma-Labyrinten i fig. ra14 i afsnit 3A).
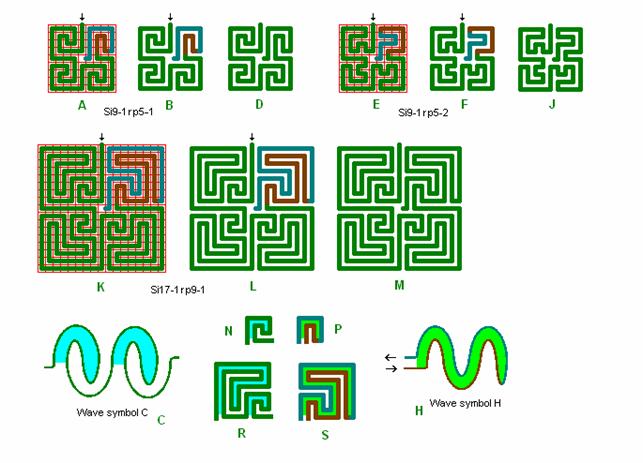
Fig. r5: Si9-1 og
Si17-1
Roma labyrinter størrelse 9 kvadrat og 17 kvadrat sammensat af grund-kvadranter fra ovenstående fig. r2 og r3.
Si9 i A, B, og D og Si17 har bølgeform C, og i kvadrant 4 bølgeform H.
Si9 i E, F, og J har bølgeform B og H, se også Si9-3 i fig. r7 nedenfor med bølgeformen.
Ved at se på labyrintbilledet i detail D, J og M kan man så vurdere om 4. kvadrant passer smukt med de øvrige kvadranter i et hurtigt helhedsindtryk.
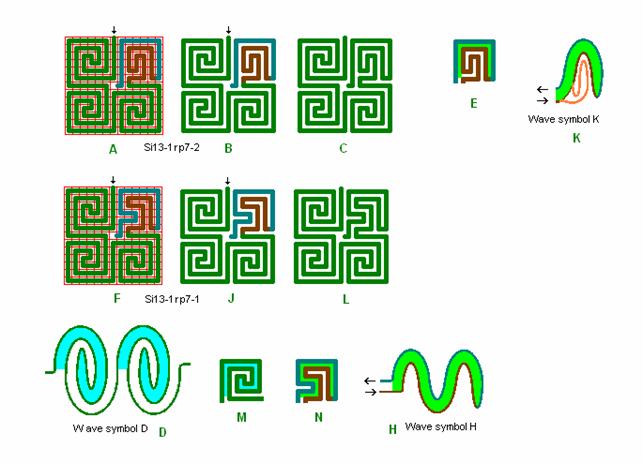
Fig. r6: Si13-1
Roma labyrint størrelse 13 kvadrat med bølgeform D og H, og med D og K.
Den nedre labyrint i detail F, Si13-1rp7-1, er sammensat af grundkvadranter fra oversigten fig. r2 og r3, med bølgeform H.
Den lidt anderledes labyrint ovenfor i detail A, Si13-1rp7-2, er sammensat af grundkvadranter fra oversigten fig. r2 og r4, med bølgeform K, hvor bølgeform K i detail K har en lille afvigelse fra dobbeltlinien i bølgeform H for at give en lille ændring til kvadrant 4 i detail E. Jeg synes den er en mere smuk roma labyrint med bedre lighed og symmetri mellem fx 1. og 4. kvadrant.
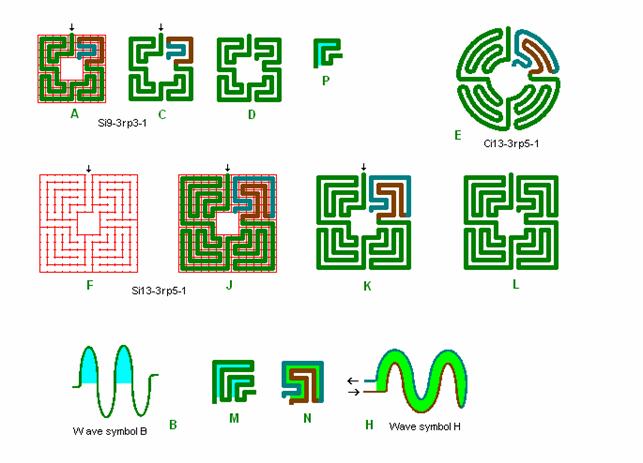
Fig. r7: Si9-3 og Si13-3
Roma labyrint størrelse 9 og 13 kvadrat efter bølgeform B og H og med midterplads.
Si 9 og 13 kvadrant med bølgeform B og C kan uden videre få bortskåret disse tern til midterområdet, mens det ikke er så enkelt for bølgeform D benyttet i forrige figur (fig. r6).
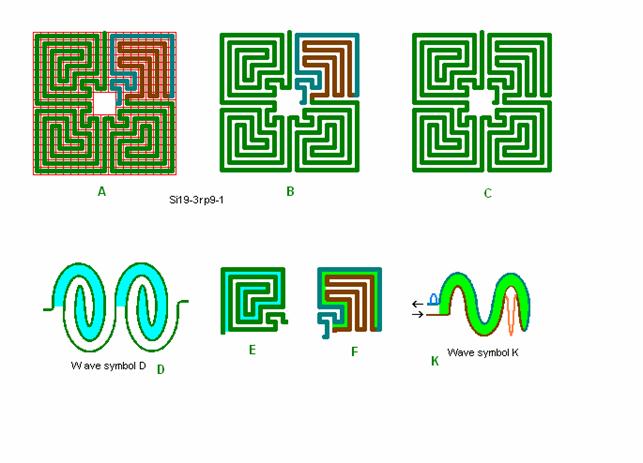
Fig. r8: Si19-3
Roma labyrint størrelse 19 kvadrat efter bølgeform D og K og med midterplads 3 x 3.
19 er ikke den helt enkle standardstørrelse for kvadrant 4, og bølge D er ikke den helt enkle form til udskæring af midterplads, men her er det gjort. Det ses at man forholdsvis nemt kan udskære en midterplads 5 x 5 stor, til Si19-5rp.
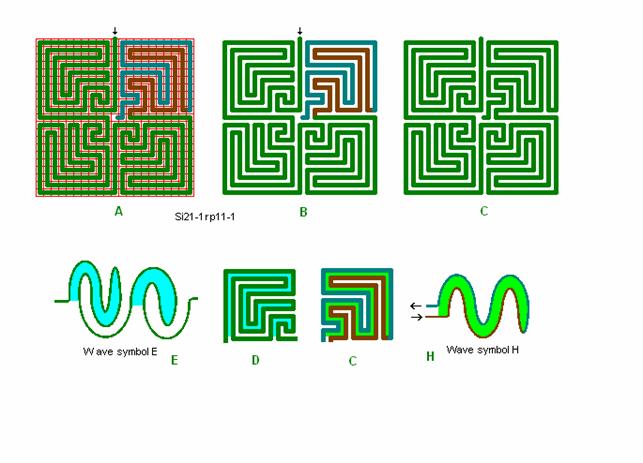
Fig. r9: Si21-1, -1
Roma labyrint størrelse 21 kvadrat efter bølgeform E og H.
Ønskes fx en plads i midten på 3 x 3 tern fås det ved en ganske lille ændring af baneforløbet i kvadrant 1 – 3 som vist i den tidligere figur med Si13-3rp5-1, eller som vist med den ægte Roma-Piadena Labyrint Si21-3rp9-1.
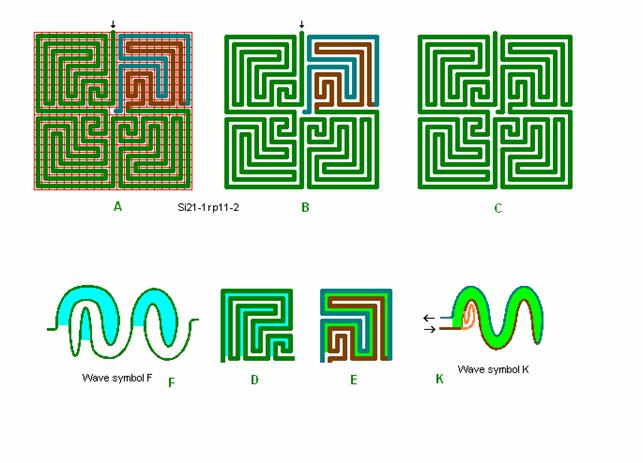
Fig. r10: Si21-1, -2
Roma labyrint størrelse 21 kvadrat efter bølgeform F og K.
Her kan der som i den forrige figur laves en plads i midten på 3 x 3 tern fx til sammenligning med den ægte Roma-Piadena Labyrint.
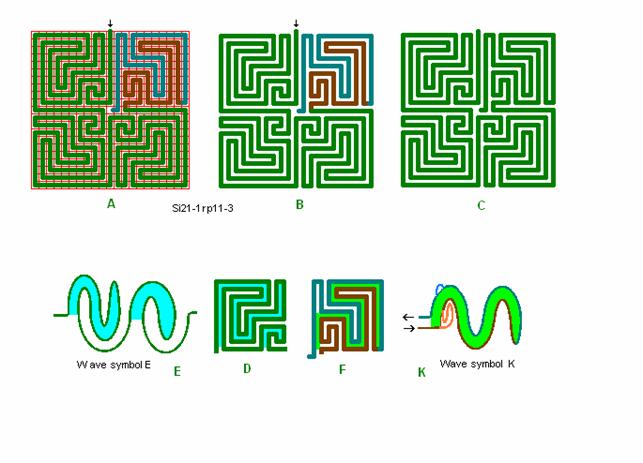
Fig. r11: Si21-1, -3
Roma labyrint størrelse 21 kvadrat efter bølgeform E og K.
Labyrinten har ikke en ubrudt yderkant (”bølgeryg”) idet den opadrettede bølge-tungespids i E ”bryder igennem”, så på det punkt opfylder den ikke helt vores roma princip (roma-piadena princip). Den kan dog ret nemt rettes til ved at trække tungespidsen lidt tilbage. Men ellers er dette jo blot et eksempel på en anderledes labyrint.
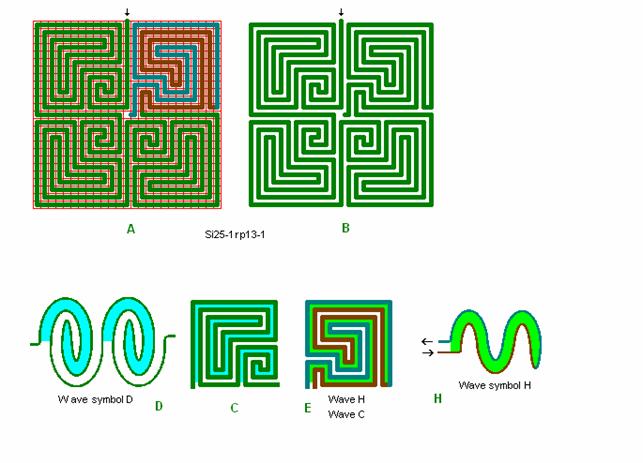
Fig. r12: Si25-1, -1
Roma labyrint størrelse 25 kvadrat efter bølgeform D og med bølgeform H og C i 4. kvadrant.
Se næste figur (fig. r13) med ændret (og smukkere) 4. kvadrant.
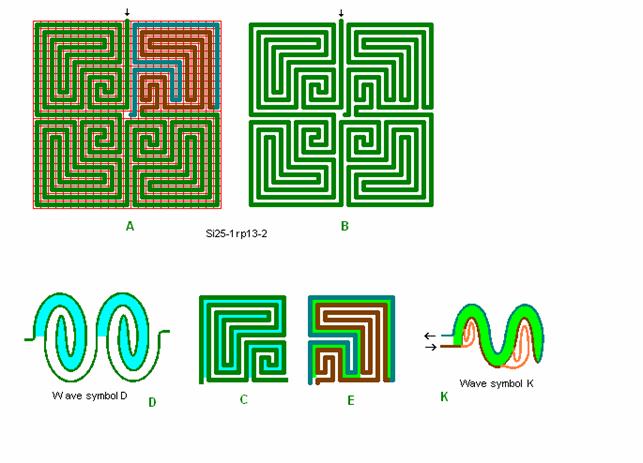
Fig. r13: Si25-1, -2
Roma labyrint størrelse 25 kvadrat efter bølgeform D og K.
Fig. r14: Si29-3
Roma labyrint størrelse 29 kvadrat efter bølgeform D og H og med midterplads.
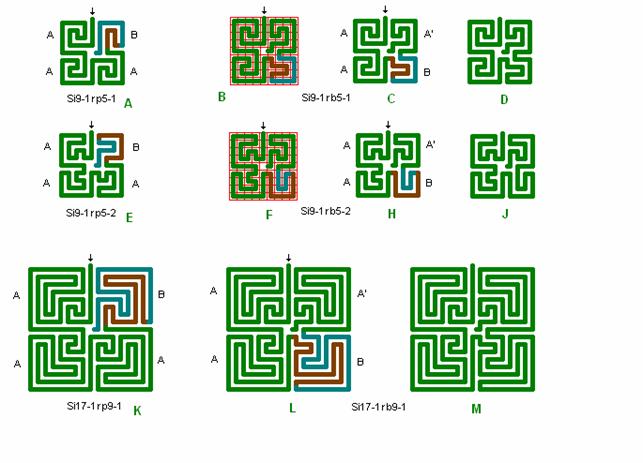
Fig. r15:Form AABA
Si9-1, Si17-1
Roma labyrinter med gennemløb af de 4 kvadranter efter formen A,A,B,A’.
I musikken benyttes ofte formen AABA. Roma labyrinter har formen AAAB. Her er vist eksempel på ændring af formen AAAB til AABA’ for 3 roma labyrinter. A’ er spejlvendt af A og A’ gennemløbes i modsat retning af A idet gennemløbsretning vendes i B.
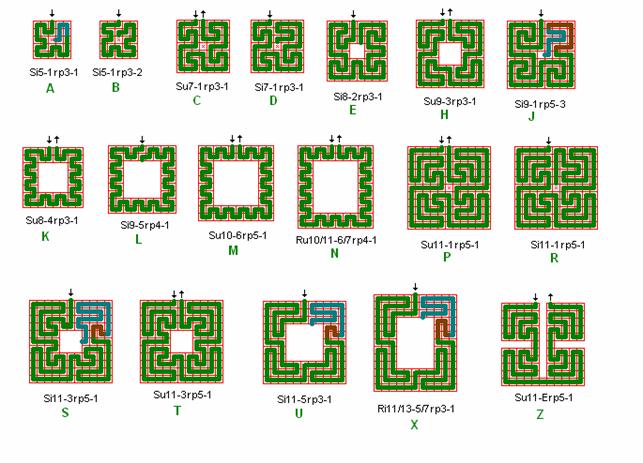
Fig. r16: Diverse roma labyrinter.
Foruden de labyrinter vi har gennemgået i det foregående kan der tegnes mange flere der mere eller mindre opfylder roma reglerne. Her er vist nogle få, med enkelte kommentarer.
Si5 i A mangler kvadrantlinie i kvadrant 4 og i B i kvadrant 1.
Si7 i D mangler en kvadrantlinie.
K, L, M, N viser en 2 bred bord og det er for smalt til roma princippet.
H, U, X viser en 3 bred bord og så kan roma princippet opfyldes. H, U, X kan let udvides til andre størrelser kvadrater og rektangler med 3 bred bord.
Su11 i Z er blot taget med for at antyde hvorledes man kan gå videre med at ”udvide” labyrinterne til at inkludere fx bælter til beplantning, sandkasser osv.
Der kan tegnes mange flere forslag til labyrinter, så ofte kan man finde en løsning der passer til de givne forhold.
Indhold af øvrige afsnit:
5 Chartres
Labyrinten i Chartres
7 Sammenlignende labyrint-eksempler