5. Chartres Labyrinten i Chartres
Labyrinten i Chartres Katedralen fra ca. år 1200 er en cirkelformet fliselabyrint i gulvet. Den er stor og gangforløbet virker umiddelbart klart og enkelt men viser sig at være uoverskueligt og uforudsigeligt som beskrevet af Jørgen Thordrup i 2002 i bogen ”Alle tiders labyrinter”. Jeg har her desuden tegnet den 11 cirkelbane store labyrint i den mere ”flisevenlige” kvadratiske form og det gør den endnu vanskeligere at overskue. Men bliver baneforløbet ”rettet ud” til en systemfigur som vist i følgende figur i detail C bliver baneforløbet klar til en overskuelig analyse. Jeg har nederst, i fig. C4 vist hvorledes Chartres Labyrinten består af en ret simpel grundfigur og hvormed man kan opbygge en række større chartres labyrinter.
Symboler og mål
Se afsnittet om labyrinter i roma stil.
Indholdsfortegnelse for figurer
Fig.
C1: Chartres Labyrinten og dets system
Fig.
C3: gennemløb i 4 afdelinger
Fig.
C4: Chartres opbygget af grundfigur ch5
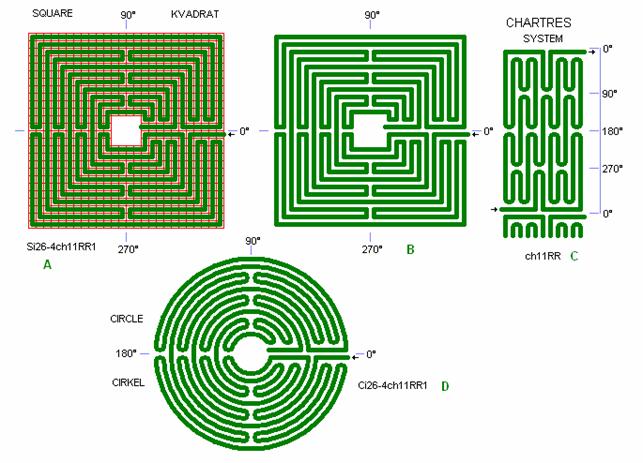
Fig. C1: Chartres
Labyrinten og dens system
Chartres Labyrinten i Chartres er her optegnet i kvadratform og cirkelform og vist i system-form i detail C. Se foto i fig. i4 i afsnit 1.
Der er her benyttet samme streg og bane-afstand som i øvrige tegninger af chartres og roma labyrinter på denne website. (Labyrinten i Chartres katedralen har smallere mellemrum mellem banerne, hvilket giver smukkere tungespidser). Chartres Labyrinten er 11 baner bred fra midt til yderkant. Den består af ”tunger” der er 90° og 180° lange, samt af 2 radiær-linier ved 0° fra yderkant til inderkant. I kvadrantlinierne 90°, 180°, og 270° er der flot symmetri med skiftevis tunge og linie forløb. Ved de 2 radiær-linier i 0° er symmetrien forskudt med én bane, så her skal det interessante opleves med: ”først se til venstre så se til højre” idet man går ind mod midten dels som start på den lange tur i venstre radiær-bane og igen til afslutning i højre radiær-bane.
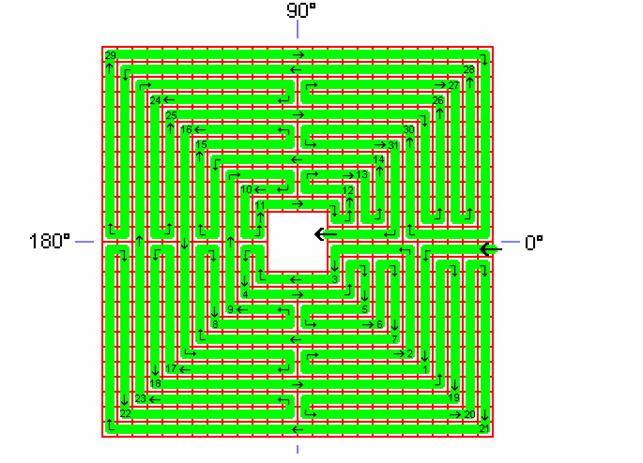
Fig. C2:
bane-gennemløb
Chartres Labyrinten som kvadrat med angivelse af bane-gennemløb.
Dette ses bedre på system-figuren:
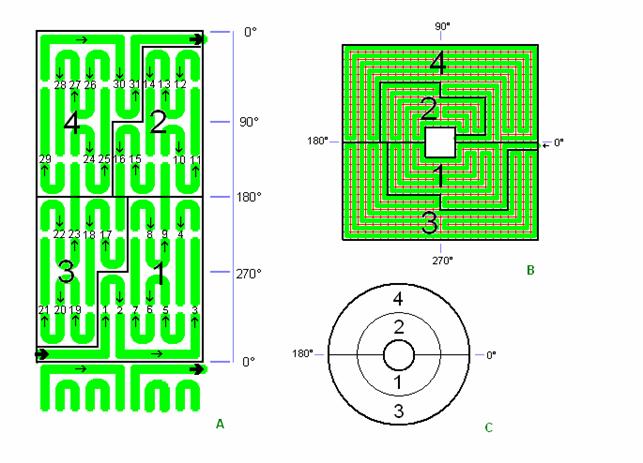
Fig. C3: gennemløb i 4
afdelinger
Chartres Labyrintens bane-gennemløb sker efter tur i 4 afdelinger.
Fra start ved udvendig kant ledes man straks (som i roma-labyrinten) af en radiær-bane ind til inderkant ved målet, dog med en enkelt tur ud i en 90° tunge midtvejs. Labyrint-området gennemløbes efter tur i 4 stk. 180° områder som vist oversigtsmæssigt på cirklen i detail C og vist præcist i detail A og B. Først gennemløbes de to inderområder og derefter de længere yderområder, hvor man til sidst fra yderbanen føres radiært ind til målet i centrum. (Denne lange tur kan i Chartres Katedralen have foregået som en pilgrimsvandring på knæ ind til det specielt hellige midterområde).
Chartres banegennemløbet kan evt. ses animeret på denne website fra Hawai.
Chartres Labyrinten er uovertruffen interessant og smuk med de flotte tunge-symmetrier i kvadrantlinierne 90°, 180°, og 270° hvor vi har tunge streg tunge streg. Måske vil nogen så spørge til symmetrien ved 0° og med de to radiærbaner her. Disse to radiærbaner er begge ”nødt til” midtvejs at have en lille tur ud i en solitude-tunge for at helheden i denne labyrint kan gå op (se fig. C4), men det er vel kun en ekstra skønhed ved denne dejlige klassiske labyrint.
Chartres Labyrinten danner grundlag for et helt system af chartres labyrinter og jeg har på denne website i afsnit 6 fx medtaget en chartres model med kun 8 baner (ch8E) og kun én radiær-bane som ligeledes har symmetri ved de 3 kvadrantlinier med skiftevis tunge og linie forløb. Desuden har den ens 90° og 270° samt tungesymmetri ved også 0°.
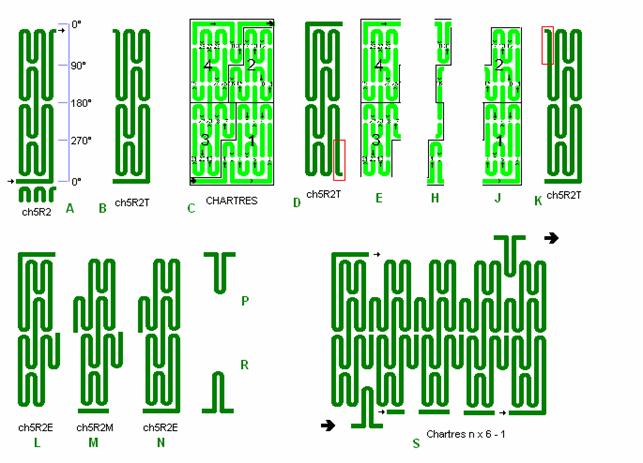
Fig. C4: Chartres
opbygget af grundfigur ch5
I afsnit 6 labyrinter i chartres stil er der i fig. ch1 vist nogle grundsystemer til chartres labyrinter. ch5R2 benyttes til at indgå i den ægte Chartres Labyrint som vist her. ch5R2 i detail A får drejet øverste halvdel til ch5R2T i B. I C har vi Chartres baneforløb fra fig. C3 ovenfor, som deles op i E, H og J. Herved ses det at Chartres Labyrinten er opbygget af ch5R2T ændret til ch5R2E i L og N samt af 2 stk. solitude-tunger på radiærbanerne som i P og R.
Af ch5R2T fås ligeledes mellemstykket ch5R2M i detail M. Dermed kan der opbygges en variabel stor chartres labyrint af de to endestykker L og N + nogle mellemstykker M, fx som vist i S en chartres 29 med 3 mellemstykker så n = 5. I alle mellemrum skal der så indskydes en radiærbane-tunge P og R, her i alt 4 på startbanen + 4 på slutbanen. Ligesom den ægte Chartres Labyrint har denne labyrint i kvadrantlinierne 90°, 180°, 270° det smukke forløb med tunge streg tunge streg.
Den ægte Chartres Labyrint består kun af de to endestykker L og N uden mellemstykker, dvs. n = 2 giver 2 x 6 - 1 = ch11.
Indhold af øvrige afsnit: